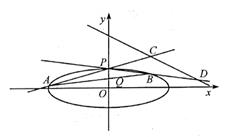
1.
已知椭圆 :
: 的离心率为
的离心率为 , 过点
, 过点 的直线
的直线 交
交 于点
于点 ,
,  , 且当
, 且当 轴时,
轴时, .
.
(1)
求 的方程
(2)
记
的方程
(2)
记 的左焦点为
的左焦点为 , 若过
, 若过 ,
,  ,
,  三点的圆的圆心恰好在
三点的圆的圆心恰好在 轴上,求直线
轴上,求直线 的斜率.
的斜率.
【考点】
直线与圆锥曲线的综合问题;