1.
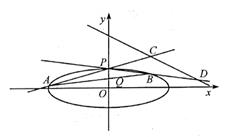
如图,已知椭圆  .设A,B是椭圆上异于
.设A,B是椭圆上异于  的两点,且点
的两点,且点  在线段
在线段  上,直线
上,直线  分别交直线
分别交直线  于C,D两点.
于C,D两点.
(Ⅰ)求点P到椭圆上点的距离的最大值;
(Ⅱ)求 的最小值.
【考点】
椭圆的简单性质;
直线与圆锥曲线的综合问题;
能力提升
变式训练
拓展培优
真题演练