1.
已知O为坐标原点,双曲线C: (
( ,
, 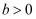 )的左顶点为A , 右焦点为F , 过A且平行于y轴的直线与C的一条渐近线交于点B , 过B且平行于x轴的直线与y轴交于点D , 若
)的左顶点为A , 右焦点为F , 过A且平行于y轴的直线与C的一条渐近线交于点B , 过B且平行于x轴的直线与y轴交于点D , 若 , 则C的离心率等于( )
, 则C的离心率等于( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
双曲线的简单性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练

