1.
数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性,形(几何)侧重研究物体形的方面,具有直观性.“以形释数”是利用数形结合思想证明代数问题的一种体现,做整式的乘法运算时,利用几何直观的方法和面积法获取结论,在解决整式运算问题时经常运用.

【问题探究】
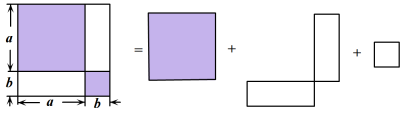
探究1:如图1所示,大正方形的边长是 , 它是由两个小正方形和两个长方形组成,所以大正方形的面积等于这四个图形的面积之和.根据等积法,我们可以得出结论:
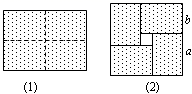
探究2:请你根据探究1所使用的等积法,从图2中探究出的结果.
【形成结论】
(1)探究2中 ;
【应用结论】
(2)利用(1)问所得到的结论求解:
已知 ,
, 求
的值;
【拓展应用】
(3)在(2)的条件下,求的值.
【考点】
完全平方公式的几何背景;