1.
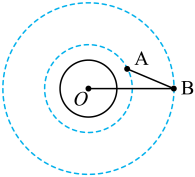
如图,半径为R的圆周上对称的分布两个质点m , 在引力的作用下二者同时运动到圆心O。计算这个运动时间可首先做如下等效:认为圆心O处有一质量为 的质点,两个质点m运动到圆心的时间可以等效为m向
的质点,两个质点m运动到圆心的时间可以等效为m向 的质点靠近的过程所用时间(
的质点靠近的过程所用时间( 不动),m向
不动),m向 的质点靠近的过程可认为是m在围绕
的质点靠近的过程可认为是m在围绕 的质点做椭圆运动(短轴极小)。已知引力常量为G , 则对于更多质点的情形,下列说法正确的是( )
的质点做椭圆运动(短轴极小)。已知引力常量为G , 则对于更多质点的情形,下列说法正确的是( )

A.
若圆周上均匀分布3个质点,则质点运动到中心的时间为 B.
若圆周上均匀分布3个质点,则质点运动到中心的时间为
B.
若圆周上均匀分布3个质点,则质点运动到中心的时间为 C.
若圆周上均匀分布n个质量为m的质点,n越大,质点运动到中心O所需的时间越短
D.
若圆周上均匀分布n个质量为m的质点,n越大,质点运动到中心O所需的时间越长
C.
若圆周上均匀分布n个质量为m的质点,n越大,质点运动到中心O所需的时间越短
D.
若圆周上均匀分布n个质量为m的质点,n越大,质点运动到中心O所需的时间越长
【考点】
开普勒定律;
万有引力定律的应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练