1.
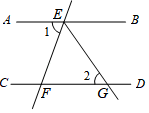
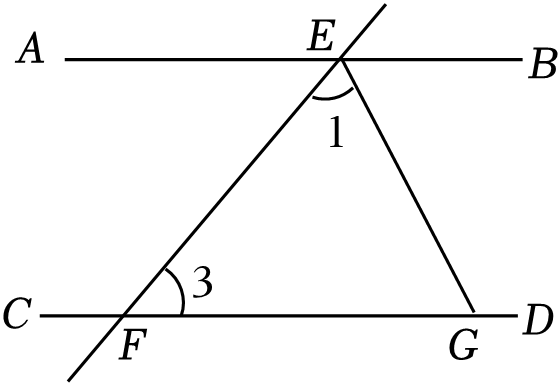
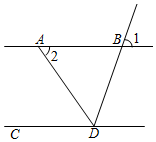
如图,直线AB∥CD , AD平分∠BDC , ∠1=70°,那么∠2的度数是( )
A.
70°
B.
65°
C.
60°
D.
55°
【考点】
平行线的性质;
角平分线的概念;