1.
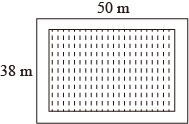
如图,在长为50m、宽为38m的矩形地面内的四周修筑同样宽的道路,余下的铺上草坪,要使草坪的面积为1260m²,道路的宽应为多少?

【考点】
一元二次方程的应用-几何问题;