1.
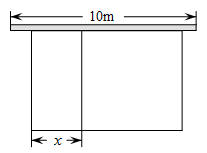
如图,老李想用长为 的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个
的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个 宽的门.(建在EF处,另用其他材料)
宽的门.(建在EF处,另用其他材料)

(1)
当羊圈的长和宽分别为多少米时,能围成一个面积为 的羊圈?
(2)
羊圈的面积能达到
的羊圈?
(2)
羊圈的面积能达到 吗?如果能,请给出设计方案;如果不能,请说明理由.
吗?如果能,请给出设计方案;如果不能,请说明理由.
【考点】
一元二次方程的应用-几何问题;