1.
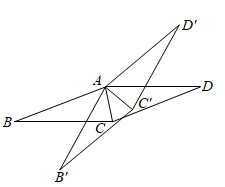
如图1,将一张菱形纸片ABCD(∠ADC>90°)沿对角线BD剪开,得到△ABD和△BCD,再将△BCD以D为旋转中心,按逆时针方向旋转角α,使α=2∠ADB,得到如图2所示的△DB′C,连接AC,BB′,∠DAB=45°,有下列结论:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= AB.其中正确结论的序号是.(把所有正确结论的序号都填在横线上)
AB.其中正确结论的序号是.(把所有正确结论的序号都填在横线上)

【考点】
菱形的性质;
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练