1.
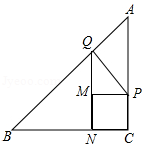
如图,在Rt△ABC中,AC=28,BC=21,一个动点P从点A出发,以每秒1个单位的速度向点C运动,同时另一个动点Q从点B出发,以每秒2个单位的速度向点A运动,当一个点运动到达终点时另一个点也随之停止运动,运动时间为ts.

(1)
用含t的代数式表示线段AQ和CP;
(2)
t为何值时,AP=AQ?
(3)
在动点P,Q的运动过程中,判断AP与BP能否相等,并说明理由.
【考点】
勾股定理;
三角形-动点问题;