1.
旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)
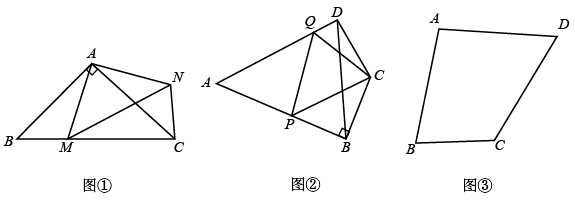
尝试解决:如图①,在等腰  中,
中,  ,点M是
,点M是  上的一点,
上的一点,  ,
,  ,将
,将  绕点A旋转后得到
绕点A旋转后得到  ,连接
,连接  ,则
,则 
 .
(2)
类比探究:如图②,在“筝形”四边形
.
(2)
类比探究:如图②,在“筝形”四边形  中,
中,  于点B ,
于点B ,  于点D , 点P、Q分别是
于点D , 点P、Q分别是  上的点,且
上的点,且  ,求
,求  的周长.(结果用a表示)
(3)
拓展应用:如图③,已知四边形
的周长.(结果用a表示)
(3)
拓展应用:如图③,已知四边形  ,
,  ,求四边形
,求四边形  的面积.
的面积.
【考点】
勾股定理;
几何图形的面积计算-割补法;
三角形的综合;
三角形-动点问题;


