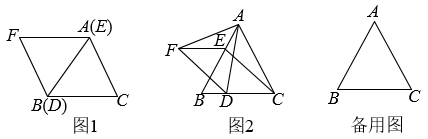
1.
等腰 中,
中, ,
,  , 点
, 点 为平面内一点,连接
为平面内一点,连接 , 将线段
, 将线段 绕点
绕点 逆时针旋转
逆时针旋转 得到线段
得到线段 .
.


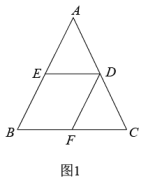
(1)
如图 , 连接
, 连接 、
、 , 若
, 若 、
、 、
、 三点共线,
三点共线, , 当
, 当 时,求
时,求 的值;
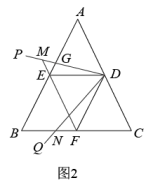
(2)
如图
的值;
(2)
如图 , 连接
, 连接 并延长至点
并延长至点 , 以
, 以 为斜边构造
为斜边构造 ,
,  交
交 于点
于点 , 连接
, 连接 , 已知
, 已知 ,
,  ,
,  , 求
, 求 的最小值.
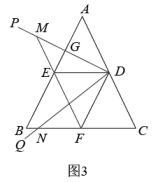
(3)
如图
的最小值.
(3)
如图 , 连接
, 连接 、
、 , 点
, 点 为
为 上一点,连接
上一点,连接 , 若
, 若 , 求证:点
, 求证:点 是
是 的中点;
的中点;
【考点】
三角形的综合;