1.
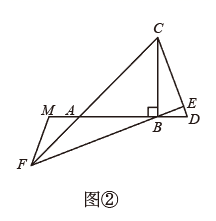
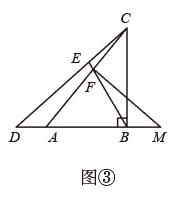
如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α.

(1)
如图,当P与E重合时,求α的度数.
(2)
当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
【考点】
翻折变换(折叠问题);
三角形的综合;
三角形-动点问题;
能力提升