1.
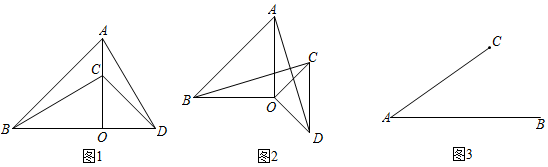
如图,在 中,
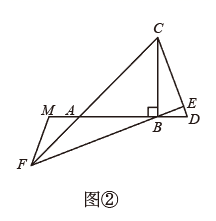
中, , 将
, 将 绕点C顺时针旋转
绕点C顺时针旋转 得到
得到 , 连接
, 连接 , 作
, 作 于点E,直线
于点E,直线 交射线
交射线 于点F.
于点F.

(1)
请直接写出线段 之间的数量关系;
(2)
当
之间的数量关系;
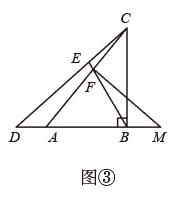
(2)
当 位于如图所示位置时,猜想线段
位于如图所示位置时,猜想线段 之间的数量关系,并证明你的结论;
(3)
请直接写出
之间的数量关系,并证明你的结论;
(3)
请直接写出 的最大值.
的最大值.
【考点】
三角形的综合;
三角形-动点问题;
能力提升
真题演练