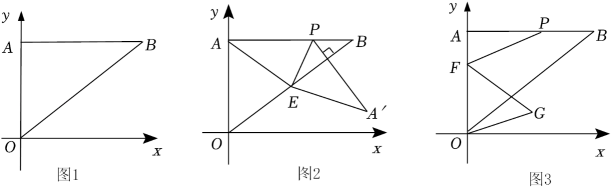
1.
在△ABC中,AB=AC , 点D为BC的中点,点E、F分别在边AB、AC上,且满足DE⊥DF .

(1)
如图1,当∠BAC=120°时,若DF∥AB , DE=m , 则DF=;
(2)
如图2,当∠BAC=90°时,求证:BE2+CF2=2DE2;
(3)
如图3,当∠BAC=60°时将∠CDF沿DF翻折,CD边与EF交于点G , 若BE=12,CF=20,求EF的长.
【考点】
翻折变换(折叠问题);
三角形的综合;