如图1，在平面直角坐标系中，Rt△OAB的直角边OA在y轴的正半轴上，且OA=6，斜边OB=10，点P为线段AB上一动点.

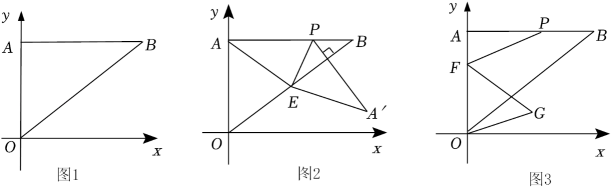
1. 如图1，在平面直角坐标系中，Rt△OAB的直角边OA在y轴的正半轴上，且OA=6，斜边OB=10，点P为线段AB上一动点.

(1) 请直接写出点B的坐标；

(2) 若动点P满足∠POB=45°，求此时点P的坐标；

(3) 如图2，若点E为线段OB的中点，连接PE，以PE为折痕，在平面内将△APE折叠，点A的对应点为A'，当PA'⊥OB时，求此时点P的坐标；

(4) 如图3，若F为线段AO上一点，且AF=2，连接FP，将线段FP绕点F顺时针方向旋转60°得线段FG，连接OG，当OG取最小值时，请直接写出OG的最小值和此时线段FP扫过的面积.

【考点】

扇形面积的计算; 翻折变换（折叠问题）; 锐角三角函数的定义; 旋转的性质; 三角形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在矩形 $\text{[math]}$ 中，E是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折得到 $\text{[math]}$ ．

(1) 如图1，若 $\text{[math]}$ ， $\text{[math]}$ ，当点F在矩形对角线 $\text{[math]}$ 上时，求 $\text{[math]}$ 的长．

(2) 如图2，当点F在 $\text{[math]}$ 上时， $\text{[math]}$ ，求证： $\text{[math]}$ ．

(3) 如图3，若 $\text{[math]}$ ，延长 $\text{[math]}$ ，与 $\text{[math]}$ 的平分线交于点G， $\text{[math]}$ 交 $\text{[math]}$ 于点，求 $\text{[math]}$ 的值．

综合题普通

2. 已知：如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，其中 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 所在的直线折叠得到 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) ①当 $\text{[math]}$ 时， $\text{[math]}$ ．

②当 $\text{[math]}$ 时， $\text{[math]}$ （用含 $\text{[math]}$ 的代数式表示）；

(2) 如图2，当 $\text{[math]}$ 时，解决以下问题：

①已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

②证明： $\text{[math]}$ ．

综合题困难

3. 将一个矩形纸片 $\text{[math]}$ 放置在平面直角坐标系中，点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上的动点（点 $\text{[math]}$ 不与点 $\text{[math]}$ ， $\text{[math]}$ 重合），连接 $\text{[math]}$ ．

(1) 如图①，当 $\text{[math]}$ 时，求点 $\text{[math]}$ 的坐标；

(2) 沿 $\text{[math]}$ 折叠该纸片，点 $\text{[math]}$ 的对应点为 $\text{[math]}$ ，设 $\text{[math]}$ ，折叠后的图形与矩形 $\text{[math]}$ 重叠部分的面积为 $\text{[math]}$ ．

①如图②，当点 $\text{[math]}$ 在第四象限时， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，试用含有 $\text{[math]}$ 的式子表示 $\text{[math]}$ ，并直接写出 $\text{[math]}$ 的取值范围；

②当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围．

综合题困难