1.
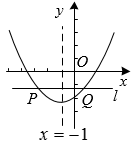
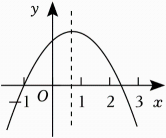
已知二次函数y=ax2+bx+c的部分图象如图所示.有以下结论:①abc<0;②a+c>0:③4a+2b+c<0;④a+b>0.其中正确的有( )
A.
4个
B.
3个
C.
2个
D.
1个
【考点】
二次函数图象与系数的关系;
二次函数图象上点的坐标特征;
基础巩固
能力提升
变式训练
拓展培优
真题演练