1.
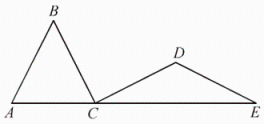
如图,AB,BC,CD,DE是四根长度均为5cm的火柴棒,点A,C,E共线.若AC=6,CD⊥BC,则线段CE的长度是( )
A.
6cm
B.
7cm
C.
 cm
D.
8cm
cm
D.
8cm
【考点】
等腰三角形的性质;
三角形全等的判定-AAS;