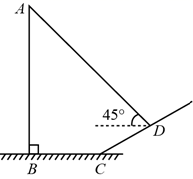
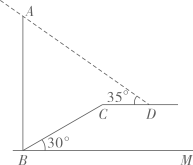
1.
如图,在一个坡度 或坡比
或坡比 :
: 的山坡
的山坡 上发现有一棵古树
上发现有一棵古树 测得古树底端
测得古树底端 到山脚点
到山脚点 的距离
的距离 米,在距山脚点
米,在距山脚点 水平距离
水平距离 米的点
米的点 处,测得古树顶端
处,测得古树顶端 的仰角
的仰角 古树
古树 与山坡
与山坡 的截面、点
的截面、点 在同一平面上,古树
在同一平面上,古树 与直线
与直线 垂直
垂直 , 求古树
, 求古树 的高度
的高度 参考数据:
参考数据: ,
,  ,
, 
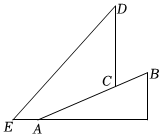
【考点】
勾股定理;
解直角三角形的实际应用﹣仰角俯角问题;