已知平行四边形ABCD，对角线AC、BD相交于点O，且CA=CB，延长BC至点E，使CE=BC，连接DE．

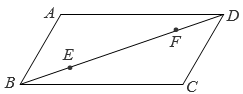
1. 已知平行四边形ABCD，对角线AC、BD相交于点O，且CA=CB，延长BC至点E，使CE=BC，连接DE．

(1) 当AC⊥BD时，求证：BE=2CD；

(2) 当∠ACB=90°时，求证：四边形ACED是正方形．

【考点】

平行四边形的判定与性质; 菱形的判定; 矩形的判定; 正方形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点 $\text{[math]}$ 的直线 $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ．

(2) 当 $\text{[math]}$ 为 $\text{[math]}$ 的中点，四边形 $\text{[math]}$ 是什么特殊四边形？请说明理由．

(3) 若 $\text{[math]}$ 为 $\text{[math]}$ 的中点，则当 $\text{[math]}$ 的度数是多少时，四边形 $\text{[math]}$ 是正方形？请说明理由．

解答题困难

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 是 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 作 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的延长线相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是平行四边形；

(2) 当 $\text{[math]}$ 满足什么条件时，四边形 $\text{[math]}$ 是菱形？请说明理由．

解答题普通

3. 如图，将 $\text{[math]}$ 的边AB延长到点E ，使 $\text{[math]}$ ，连结DE ，交边BC于点F ．

(1) 求证： $\text{[math]}$ ．

(2) 连结BD ， CE ．若 $\text{[math]}$ ，求证：四边形BECD是矩形．

解答题普通