1.
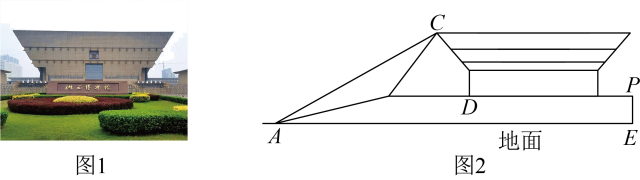
山西博物院是我省综合性博物馆之一,其主馆造型如斗似鼎,四翼舒展,诠释了“如鸟斯革,如翚斯飞”的审美取向.某校“综合实践”小组在项目化学习中,对主馆进行了实地测量,图2是测量示意图.他们在地面上的 点测得主馆顶部
点测得主馆顶部 的仰角为
的仰角为 , 在台阶顶部
, 在台阶顶部 处测得主馆顶部
处测得主馆顶部 的仰角为
的仰角为 , 经过对每个台阶的高度与宽度进行测量,确定台阶顶部
, 经过对每个台阶的高度与宽度进行测量,确定台阶顶部 到地面的高度为12米,台阶底部
到地面的高度为12米,台阶底部 与顶部
与顶部 之间的水平距离为30米.现已知台阶顶部平台
之间的水平距离为30米.现已知台阶顶部平台 与地面
与地面 平行.请根据以上数据,求出主馆顶部
平行.请根据以上数据,求出主馆顶部 到地面的垂直高度是多少米?(参考数据:
到地面的垂直高度是多少米?(参考数据: ,
,  ,
,  )
)
【考点】
锐角三角函数的定义;
解直角三角形的实际应用﹣仰角俯角问题;