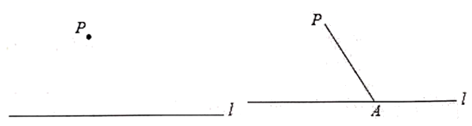1.
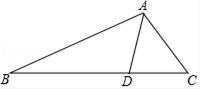
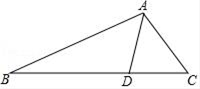
如图,在  中,
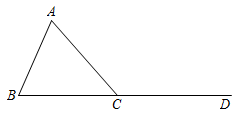
中,  为
为  的外角.
的外角.

(1)
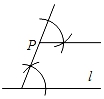
尺规作图:作  的平分线
的平分线  (保留作图痕迹可加黑,不写作法);
(2)
若
(保留作图痕迹可加黑,不写作法);
(2)
若  ,在(1)的条件下,求证:
,在(1)的条件下,求证:  .
.
【考点】
平行线的判定;
尺规作图-作角的平分线;
能力提升
真题演练