1.
下面是嘉琪同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
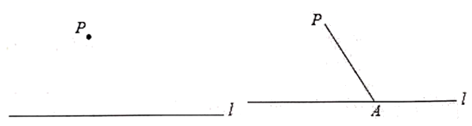
已知:如图,直线l和直线l外一点P .
求作:直线PQ , 使直线PQ 直线l .
作法:如图,
①在直线l上取一点A , 连接PA;
②作PA的垂直平分线MN , 分别交直线l , 线段PA于点B , O;
③以O为圆心,OB长为半径作弧,交直线MN于另一点Q;
④作直线PQ , 所以直线PQ为所求作的直线.
根据上述作图过程,回答问题:
(1)
用直尺和圆规,补全图中的图形(保留作图痕迹);
(2)
完成下面的证明:
证明:∵直线MN是PA的垂直平分线,
∴ ▲ = ▲ , ∠POQ=∠AOB=90°.
∴△POQ≌△AOB .
∴ ▲ = ▲ ,
∴PQ l( ▲ )(填推理的依据).
【考点】
平行线的判定;