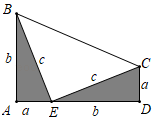
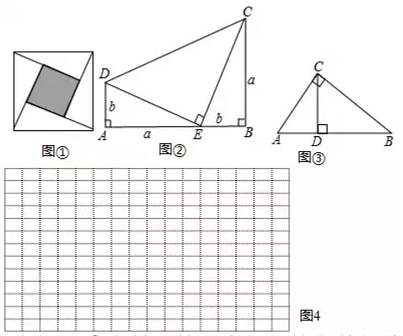
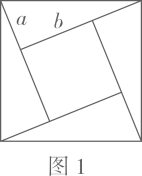
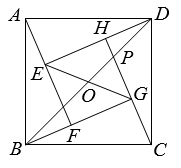
勾股定理的证明方法是多样的，其中“面积法”是常用的方法．小丽发现：当四个全等的直角三角形如图摆放时，可以用“面积法”来证明勾股定理．请写出勾股定理的内容，并利用给定的图形进行证明．

1. 现有4个全等的直角三角形(阴影部分)，直角边长分别为a、b，斜边长为c，将它们拼合为如图的形状.

(1) 添加如图辅助线，根据该图，可以用两种不同的方法计算整个组合图形的面积，通过面积相等，从而证明勾股定理，请你将下面的证明过程补充完整：

整个组合图形面积表示，方法一：以c为边的正方形的面积+两个直角三角形的面积，即最后化简为；方法二：以a和b为边的两个小正方形的面积+两个直角三角形的面积，即最后化简为；根据面积相等，直接得等式，化简最后结果是，从而证明勾股定理.

(2) 当 a=5， b=8时，求空白部分的面积.

解答题普通

2. 如图所示的是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，请你开动脑筋，将它们拼成一个能证明勾股定理的图形.

(1) 画出拼成的这个图形的示意图，并用这个图形证明勾股定理.

(2) 假设图中的直角三角形有若干个，你能运用图中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(不需要证明).

解答题普通

3. 将两个全等的直角三角形按如图所示摆放，使点A、E、D在同一条直线上．利用此图的面积表示式证明勾股定理．

解答题普通

1. 《勾股举隅》为梅文鼎研究中国传统勾股算术的著作，其中的主要成就是对勾股定理的证明和对勾股算术算法的推广．书中的证明方法是将4个边长分别为a、b、c的全等直角三角形拼成如图1所示的五边形 $\text{[math]}$ ，然后通过添加辅助线用面积法证明勾股定理．下面是小华给出的相关证明：

如图，延长 $\text{[math]}$ 交①于点G．

用两种不同的方法表示五边形 $\text{[math]}$ 的面积S：

方法一：将五边形 $\text{[math]}$ 看成是由正方形 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 拼成，则 $\text{[math]}$ ②．

方法二：将五边形 $\text{[math]}$ 看成是由③，正方形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 拼成，根据面积相等可以得到④，进而通过化简验证得出勾股定理．

则下列说法错误的是（　　）

A. ①代表 $\text{[math]}$ B. ②代表 $\text{[math]}$ C. ③代表正方形 $\text{[math]}$ D. ④代表 $\text{[math]}$

单选题容易

2. 国际数学家大会是由国际数学联盟（IMU）主办的国际数学界规模最大也是最重要的会议，它是全球性数学科学学术会议，被誉为数学界的奥林匹克盛会. 如图所示是第 24 届国际数学家大会会标，该会标取自于我国数学家赵爽注解《周髀算经》中的弦图. 与该弦图有着密切关系的数学文化是（）

A. 勾股定理的证明 B. 圆周率的估算 C. 无理数的发现 D. 黄金分割比

单选题普通

3. 根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”、“无字证明”可用于验证数与代数、图形与几何等领域中的许多数学公式和规律，体现了数形结合的思想方法，展现了数学美，下面图形验证的内容是（）

A. 乘法公式 B. 勾股定理 C. 直角三角形中边和角的关系 D. 中位线定理

单选题容易

1. 勾股定理是证明方法最多的定理之一，小明便以此建立项目，加以探究.

【问题提出】小明在做作业本时发现利用右图可以证明勾股定理.思路为利用面积法，将梯形的面积用不同的方式表示列出等式.由此猜想如果将Rt△DAF向左平移，能否证明勾股定理？

【方案设计】考虑到探究的难度，他首先设计了两种特殊的位置，开展研究：

方案	方案一	方案二
图形
备注	Rt△BCA≌Rt△EAD	Rt△BCA≌Rt△CFD
备注	BC=a，AC=b，AB=c

(1) 【探究验证】首先验证方案一为方案二提供经验基础.

方式

验证过程

（分别用含有a，b，c的代数式完成填空）

图形

方式①

S_{四边形ADBE}=S_△_ABE+S_△_ABD

S△ABE= ▲ ．（以AE为底，高为BC）

S△ABD= ▲ ．（以AD为底，则AD边上的高与AC等长）

连结BE，BD，不难得出AB⊥ED

方式②

S_{四边形ADBE}=S_△_EBD+S_△_EAD

S_△_EBD= $\text{[math]}$ EDBH，S_△_EAD=EDAH

S_△_EBD+S_△_EAD= $\text{[math]}$ EDBH＋ $\text{[math]}$ EDAH

= $\text{[math]}$ ED（BH＋AH）= $\text{[math]}$ EDAB= ▲

综上所述利用方式①，②列出等式即可证明勾股定理.

(2) 【方法应用】

根据上述经验，请你继续完成方案二后续的证明过程.提示：如图，连结BD，AD，不难得出CD⊥BA，利用两种方法表示四边形BCAD的面积.

实践探究题困难

2. 教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为 $\text{[math]}$ ，较小的直角边长都为 $\text{[math]}$ ，斜边长都为 $\text{[math]}$ ），大正方形的面积可以表示为 $\text{[math]}$ ，也可以表示为 $\text{[math]}$ ，由此推导出重要的勾股定理：如果直角三角形两条直角边长为 $\text{[math]}$ ，斜边长为 $\text{[math]}$ ，则 $\text{[math]}$ ．

(1) 图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．

(2) 如图③，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

(3) 试构造一个图形，使它的面积能够解释 $\text{[math]}$ ，画在如图4的网格中，并标出字母 $\text{[math]}$ 所表示的线段．

综合题困难

3. 数与形是数学中的两个最古老，也是最基本的研究对象．数与形也是有联系的，这种联系称为“数形结合”．利用“数形结合”思想可以直观地帮助我们解决一些数学验证或运算．

(1) 我国是最早了解勾股定理的国家之一，该定理阐明了直角三角形的三边关系．请你利用如图对勾股定理（即下列命题）进行验证，从中体会“数形结合”的思想：

已知：如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ，（点B，C，D在一条直线上）， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

证明： $\text{[math]}$ ；

(2) 请利用“数形结合”思想，画图推算出 $\text{[math]}$ 的结果．

证明题普通

1. 2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图1），且大正方形的面积是15，小正方形的面积是3，直角三角形的较短直角边为a，较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放，那么图2中最大的正方形的面积为.

填空题普通

2. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH . 连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则 $\text{[math]}$ 的值是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题困难

3. 如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．

①求证： $\text{[math]}$ ；

②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．

证明题普通