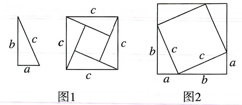
1.
勾股定理是证明方法最多的定理之一,小明便以此建立项目,加以探究.
【问题提出】小明在做作业本时发现利用右图可以证明勾股定理.思路为利用面积法,将梯形的面积用不同的方式表示列出等式.由此猜想如果将Rt△DAF向左平移,能否证明勾股定理?

【方案设计】考虑到探究的难度,他首先设计了两种特殊的位置,开展研究:
方案 | 方案一 | 方案二 |
图形 |
|
|
备注 | Rt△BCA≌Rt△EAD | Rt△BCA≌Rt△CFD |
BC=a,AC=b,AB=c | ||
(1)
【探究验证】首先验证方案一为方案二提供经验基础.
(2)
【方法应用】
方式 | 验证过程 (分别用含有a,b,c的代数式完成填空) | 图形 |
方式① | S四边形ADBE=S△ABE+S△ABD S△ABE= ▲ . (以AE为底,高为BC) S△ABD= ▲ . (以AD为底,则AD边上的高与AC等长) | 连结BE,BD,不难得出AB⊥ED
|
方式② | S四边形ADBE=S△EBD+S△EAD S△EBD= S△EBD+S△EAD= = |
综上所述利用方式①,②列出等式即可证明勾股定理.
根据上述经验,请你继续完成方案二后续的证明过程.提示:如图,连结BD,AD,不难得出CD⊥BA,利用两种方法表示四边形BCAD的面积.

【考点】
三角形的面积;
勾股定理的证明;
能力提升