1.
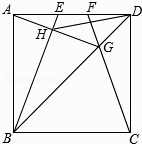
如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ﹣2.
A.
2
B.
3
C.
4
D.
5
【考点】
全等三角形的判定与性质;
正方形的性质;
相似三角形的判定与性质;
解直角三角形;