1.
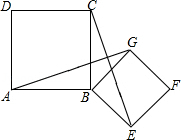
已知：⊙O是正方形ABCD的外接圆，点E在弧AB上，连接BE、DE，点F在弧AD上，连接BF，DF，BF与DE、DA分别交于点G、点H，且DA平分∠EDF.
(1)
如图1，求证：∠CBE=∠DHG；
(2)
如图2，在线段AH上取一点N（点N不与点A、点H重合)，连接BN交DE于点L，过点H作HK∥BN交DE于点K，过点E作EP⊥BN垂足为点P，当BP=HF时，求证：BE=HK；
(3)
如图3，在(2)的条件下，当3HF=2DF时，延长EP交⊙0于点R，连接BR，若△BER的面积与△DHK的面积的差为 
，求线段BR的长.
【考点】
全等三角形的判定与性质;
正方形的性质;
圆周角定理;
相似三角形的判定与性质;
解直角三角形;
