1.
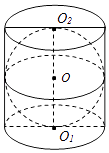
如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1 , 球O的体积为V2 , 则 的值是.
【考点】
旋转体(圆柱/圆锥/圆台/球)的结构特征;
球的表面积与体积公式及应用;
基础巩固
能力提升
变式训练
拓展培优



