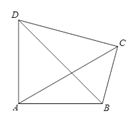
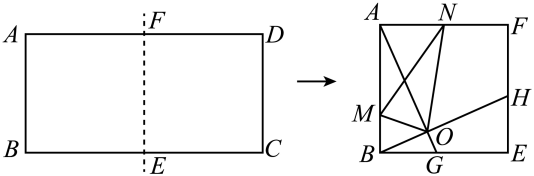
如图，在边长为的正方形中，点分别是边的中点，连接点分别是的中点，连接，则的长度为.

0 返回首页

1. 如图，在边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别是边 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 点 $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为.

【考点】

矩形的判定与性质; 正方形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

正方形的定义	有一组邻边相等，并且有一个角是的平行四边形叫做正方形.
正方形的性质	1.正方形的四条边，四个角都是，对角线互相垂直平分且相等，并且每一条对角线平分一组对角，它具有矩形和菱形的所有性质.
正方形的性质	2.正方形既是轴对称图形也是中心对称图形，对称轴有条，对称中心是对角线的交点.
正方形的判定	1.有一组邻边相等的矩形是正方形.
	2.有一个角是直角的是正方形.
	3.对角线互相垂直平分且相等的四边形是正方形.

基础知识填空容易

1. 如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S_四边形_CDFE= $\text{[math]}$ S_△_ABC ．上述结论中始终正确的有．（填序号）

填空题普通

2. 如图所示，这是一款在某商城热销的笔记本电脑散热支架，在保护颈椎的同时能让笔记本电脑更好地散热．根据产品介绍，当显示屏与水平线夹角为 $\text{[math]}$ 时为最佳健康视角．如图，小翼希望通过调试和计算对购买的散热架 $\text{[math]}$ 进行简单优化，现在笔记本电脑下垫入散热架，散热架角度为 $\text{[math]}$ ，调整显示屏 $\text{[math]}$ 与水平线夹角保持 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，若要 $\text{[math]}$ ，则底座 $\text{[math]}$ 的长度应设计为 $\text{[math]}$ ．（结果保留根号）

填空题普通

3. 如图，在四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，连接AC、BD，若S_四边形_ABCD＝18，则BD的最小值为.

填空题普通

1. 如图，▱ABCD中，对角线AC，BD相交于点O，OA＝3，若要使平行四边形ABCD为矩形，则OB的长度为（　　）

A. 4 B. 3 C. 2 D. 1

单选题容易

2. 如图，矩形纸片ABCD，AD＝4，AB＝3，如果点E在边BC上，将纸片沿AE折叠，使点B落在点F处，连接FC，当△EFC是直角三角形时，那么BE的长为( )

A. 1.5 B. 3 C. 1.5或3 D. 有两种情况以上

单选题普通

3. 下列关于矩形的说法中正确的是（）

A. 对角线相等的四边形是矩形 B. 矩形的对角线相等且互相平分 C. 对角线互相平分四边形是矩形 D. 矩形的对角线互相垂直且平分

单选题容易

1. 综合与探究：如图， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的平分线上， $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) 【操作判断】

如图①，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，根据题意在图①中画出 $\text{[math]}$ ，图中 $\text{[math]}$ 的度数为度；

(2) 【问题探究】

如图②，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 【拓展延伸】

点 $\text{[math]}$ 在射线 $\text{[math]}$ 上，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，射线 $\text{[math]}$ 与射线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

实践探究题困难

2. 如图，已知 $\text{[math]}$ ，点A是射线 $\text{[math]}$ 上一点， $\text{[math]}$ ，动点P从点A出发，以 $\text{[math]}$ 的速度沿 $\text{[math]}$ 水平向左运动，与此同时，动点Q从点O出发，也以 $\text{[math]}$ 的速度沿 $\text{[math]}$ 竖直向上运动，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为斜边向上作等腰直角三角形 $\text{[math]}$ ，设运动时间为 $\text{[math]}$ ，其中 $\text{[math]}$ ．

(1) 当 $\text{[math]}$ 与 $\text{[math]}$ 全等时，求t的值；

(2) 四边形 $\text{[math]}$ 的面积为　　．

解答题普通

3. 综合与实践

数学活动课上，数学老师以“矩形纸片的折叠”为课题开展数学活动：将矩形纸片ABCD对折，使得点A、D重合，点B、C重合，折痕为EF ，展开后沿过点B的直线再次折叠纸片，点A的对应点为点N ，折痕为BM ．

(1) 如图①，若AB＝BC ，则当点N落在EF上时，BF和BN的数量关系是；∠NBF的度数为；

(2) 思考探究：

在AB＝BC的条件下进一步进行探究，将△BMN沿BN所在的直线折叠，点M的对应点为点 $\text{[math]}$ ，当点 $\text{[math]}$ 落在CD上时，如图②，设BN、 $\text{[math]}$ 分别交EF于点J、K ，若 $\text{[math]}$ ，请求出三角形BJK的面积；

(3) 拓展应用：

如图③，在矩形纸片ABCD中，AB＝6，AD＝12，将纸片沿过点B的直线折叠，折痕为BM ，点A的对应点为点N ，展开后再将四边形ABNM沿BN所在的直线折叠，点A的对应点为点P ，点M的对应点为点 $\text{[math]}$ ，连接CP、DP ，若PC＝PD ，请直接写出AM的长．

实践探究题困难

1. 如图，把边长为1：2的矩形ABCD沿长边BC，AD的中点E，F对折，得到四边形ABEF，点G，H分别在BE，EF上，且BG＝EH＝ $\text{[math]}$ BE＝2，AG与BH交于点O，N为AF的中点，连接ON，作OM⊥ON交AB于点M，连接MN，则tan∠AMN＝.

填空题困难

2. 如图，直尺AB垂直竖立在水平面上，将一个含45°角的直角三角板CDE的斜边DE靠在直尺的一边AB上，使点E与点A重合，DE＝12cm.当点D沿DA方向滑动时，点E同时从点A出发沿射线AF方向滑动.当点D滑动到点A时，点C运动的路径长为 cm.

填空题普通

如图，在菱形ABCD中，AB=6，∠DAB=60°，AE分别交BC、BD于点E、F，CE=2，连接CF，以下结论：①△ABF≌△CBF；②点E到AB的距离是 $\text{[math]}$ ；③tan∠DCF= $\text{[math]}$ ；④△ABF的面积为 $\text{[math]}$ $\text{[math]}$ ．其中一定成立的是（把所有正确结论的序号都填在横线上）．

填空题普通