1.
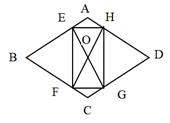
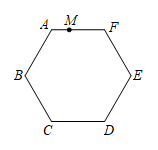
边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（ ）
A.
B.
C.
D.
【考点】
等边三角形的判定与性质;
