1.
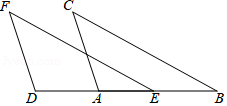
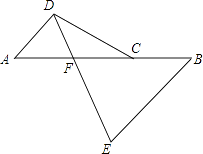
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.

【考点】
平行线的性质;
全等三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练