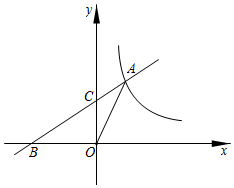
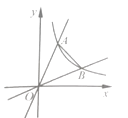
如图，直线l⊥x轴于点P，且与反比例函数y1 （x＞0）及y2= （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2=．

1.

如图，直线l⊥x轴于点P，且与反比例函数y₁ $\text{[math]}$ （x＞0）及y₂= $\text{[math]}$ （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k₁﹣k₂=．

【考点】

反比例函数系数k的几何意义; 反比例函数与一次函数的交点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 如图，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 图象上的一个点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴， $\text{[math]}$ 轴，垂足分别为 $\text{[math]}$ ， $\text{[math]}$ ，矩形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ ．

填空题容易

2. 如图是反比例函数 $\text{[math]}$ 的图象，点A(x ， y)是反比例函数图象上任意一点，过点A作AB⊥x轴于点B ，连接OA ，则△AOB的面积是.

填空题容易

3. 若正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ ，则另一个交点坐标为．

填空题容易