1.
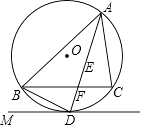
如图,△ABC内接于⊙O,AB为⊙O直径,AC=CD,连接AD交BC于点M,延长MC到N,使CN=CM.
(1)判断直线AN是否为⊙O的切线,并说明理由;
(2)若AC=10,tan∠CAD= , 求AD的长.

【考点】
切线的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练