1.
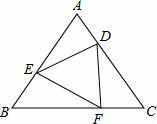
如图,已知△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.
【考点】
等边三角形的判定与性质;