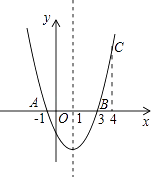1.
已知抛物线  的对称轴是直线
的对称轴是直线  ,与
,与  轴相交于
轴相交于  ,
,  两点(点
两点(点  在点
在点  右侧),与
右侧),与  轴交于点
轴交于点  .
.
(1)
求抛物线的解析式和  ,
,  两点的坐标;
(2)
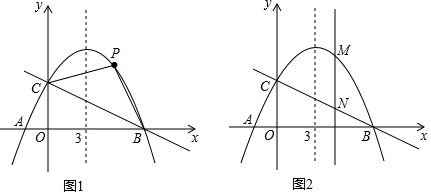
如图1,若点
两点的坐标;
(2)
如图1,若点  是抛物线上
是抛物线上  、
、  两点之间的一个动点(不与
两点之间的一个动点(不与  、
、  重合),是否存在点
重合),是否存在点  ,使四边形
,使四边形  的面积最大?若存在,求点
的面积最大?若存在,求点  的坐标及四边形 PBOC 面积的最大值;若不存在,请说明理由;
的坐标及四边形 PBOC 面积的最大值;若不存在,请说明理由;
(3)
如图2,若点  是抛物线上任意一点,过点
是抛物线上任意一点,过点  作
作  轴的平行线,交直线
轴的平行线,交直线  于点
于点  ,当
,当  时,求点
时,求点  的坐标.
的坐标.
【考点】
二次函数的最值;
二次函数图象上点的坐标特征;
二次函数y=ax²+bx+c的性质;