1.
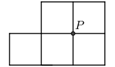
在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积. 如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A.
2 B.
B.
 C.
C.
 D.
D.

【考点】
待定系数法求一次函数解析式;
线段上的两点间的距离;








