1.
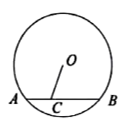
某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)

【考点】
垂径定理的实际应用;
能力提升
变式训练
拓展培优
真题演练