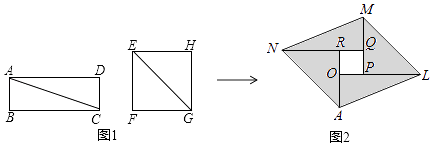1.
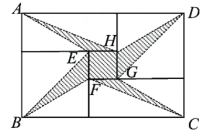
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若  ,
,  ,则该矩形的面积为( )
,则该矩形的面积为( )

A.
20
B.
24
C.
 D.
D.

【考点】
几何图形的面积计算-割补法;
基础巩固
能力提升
变式训练
拓展培优
真题演练