1.
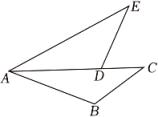
如图,D是AB上一点,DF交AC于点E , DE= FE , FC //AB.

求证:AE=CE.
证明:∵FC //AB,
∴∠A=∠ ① , ∠ADE=∠ ②
在△ADE和△CFE中,
∵
∴△ADE ≌ △CFE ( ⑤ ),
∴ ⑥
【考点】
三角形全等的判定-AAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练