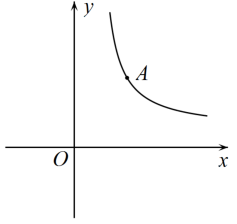1.
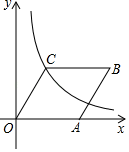
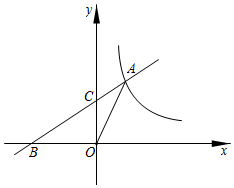
在同一直角坐标系中,一次函数 与反比例函数
与反比例函数 的图像可能是( )
的图像可能是( )
A.
 B.
B.
 C.
C.
 D.
D.

 B.
B.
 C.
C.
 D.
D.

【考点】
反比例函数与一次函数的交点问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练