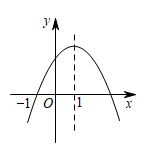如图，一位篮球运动员投篮时，球从点出手后沿抛物线行进，篮球出手后距离地面的高度与篮球距离出手点的水平距离x(m)之间的函数关系式是．下列说法正确的是（填序号）．①篮球行进过程中距离地面的最大高度为；②篮球出手点距离地面的高度为．

1. 如图，一位篮球运动员投篮时，球从 $\text{[math]}$ 点出手后沿抛物线行进，篮球出手后距离地面的高度 $\text{[math]}$ 与篮球距离出手点的水平距离x(m)之间的函数关系式是 $\text{[math]}$ ．下列说法正确的是（填序号）． $\text{[math]}$

①篮球行进过程中距离地面的最大高度为 $\text{[math]}$ ；

②篮球出手点距离地面的高度为 $\text{[math]}$ ．

【考点】

二次函数的最值; 二次函数图象与坐标轴的交点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 已知抛物线y=x²-6x+m与x轴有且只有一个交点，则m=.

填空题容易

2. 若函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴只有一个公共点，则常数 $\text{[math]}$ 的值是．

填空题容易

3. 二次函数 $\text{[math]}$ 的最小值为2，则 $\text{[math]}$ 的值为

填空题容易