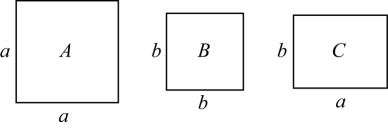
1.
如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式,你认为其中正确的有( )
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn.

A.
①②
B.
③④
C.
①②③
D.
①②③④
【考点】
多项式乘多项式;
用代数式表示几何图形的数量关系;