1.
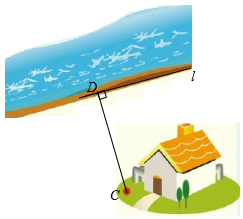
在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,他们过点C向河岸l作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是( )
A.
两点之间,线段最短
B.
过一点有且只有一条直线与已知直线垂直
C.
垂线段最短
D.
两条直线相交有且只有一个交点
【考点】
垂线段最短及其应用;