问题发现．

1. 问题发现．

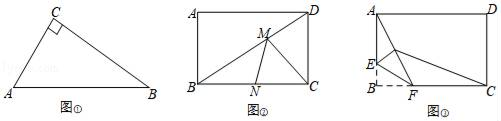
(1) 如图①，Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是AB边上任意一点，则CD的最小值为．

(2) 如图②，矩形ABCD中，AB＝3，BC＝4，点M、点N分别在BD、BC上，求CM+MN的最小值．

(3) 如图③，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是BC边上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG、CG，四边形AGCD的面积是否存在最小值，若存在，求这个最小值及此时BF的长度．若不存在，请说明理由．

【考点】

垂线段最短及其应用; 轴对称的应用-最短距离问题; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图①，要在一条笔直的路边l上建一个燃气站，向l同侧的A、B两个城镇分别发铺设管道输送燃气，试确定燃气站的位置，使铺设管道的路线最短.

(1) 如图②，作出点A关于l的对称点 $\text{[math]}$ ，线 $\text{[math]}$ 与直线 $\text{[math]}$ 的交点C的位置即为所求，即在点C处建气站，所得路线ACB是最短的，为了让明点C的位置即为所求，不妨在l直线上另外任取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，证明 $\text{[math]}$ ，请完成这个证明.

(2) 如果在A、B两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案（不需说明理由），

①生市保护区是正方形区城，位置如图③所示

②生态保护区是圆形区域，位置如图④所示.

综合题普通

(1) 如图1，在AB直线一侧有C，D两点，在AB上找一点P，使C，D，P三点组成的三角形的周长最短，找出此点并说明理由：

(2) 如图2，在∠AOB内部有一点P，是否在OA，OB上分别存在点E，F，使得E，F，P三点组成的三角形的周长最短，找出E，F两点，并说明理由：

(3) 如图3，在∠AOB内部有两点M，N，是否在OA，OB上分别存在点E，F，使得E，F， M，N，四点组成的四边形的周长最短，找出E，F两点，并说明理由.

综合题困难

3. 如图，在直角梯形AOBC中，AC∥OB，且OB=6，AC=5，OA=4.

(1) 求B、C两点的坐标：

(2) 以O、A、B、C中的三点为顶点可组成哪几个不同的三角形？

(3) 是否在边AC和BC（含端点）上分别存在点M和点N，使得△MON的面积最大时，它的周长还最短？若存在，说明理由，并求出这时点M、N的坐标；若不存在，为什么？

综合题困难