1.
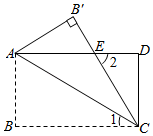
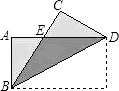
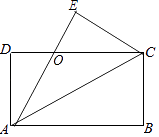
在矩形  中,
中,  2cm,将矩形
2cm,将矩形  沿某直线折叠,使点B与点D重合,折痕与直线
沿某直线折叠,使点B与点D重合,折痕与直线  交于点E,且
交于点E,且  3cm,则矩形
3cm,则矩形  的面积为cm2 .
的面积为cm2 .
【考点】
矩形的性质;
翻折变换(折叠问题);