1.
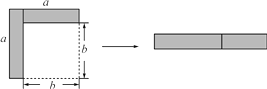
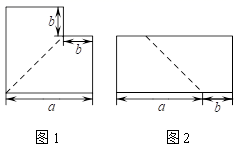
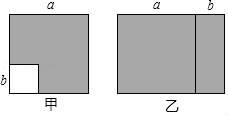
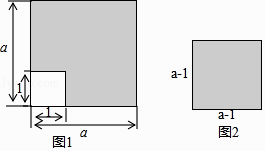
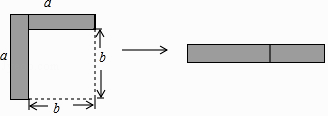
如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形.(a>0)剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)则矩形的面积为( )

A.
(2a2+5a)cm2
B.
(3a+15)cm2
C.
(6a+9)cm2
D.
(6a+15)cm2
【考点】
平方差公式的几何背景;