1.
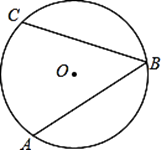
如图,CD是⊙O的直径,BE是⊙O的弦,DC,EB的延长线相交于点A,若∠EOD=75°,AB=OC,求∠A的度数.

【考点】
三角形的外角性质;
圆的相关概念;
基础巩固
能力提升
变式训练
拓展培优
真题演练