1.
数学兴趣小组探究勾股定理在折叠中的应用.如图长方形纸片 ,
,  ,
,  , 点
, 点 为长方形纸片
为长方形纸片 边
边 上一动点,连结
上一动点,连结 , 将
, 将 沿
沿 折叠,点
折叠,点 落在点
落在点 处.
处.

(1)
 的长为________.
(2)
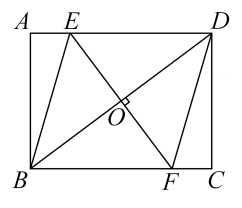
如图①,当点
的长为________.
(2)
如图①,当点 在线段
在线段 上时,求
上时,求 的长.
(3)
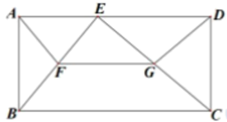
如图②,在(1)的条件下,当点
的长.
(3)
如图②,在(1)的条件下,当点 与点
与点 重合时,沿
重合时,沿 将
将 折叠得
折叠得 ,
,  与
与 交于
交于 点,则
点,则 的面积是________.
的面积是________.
【考点】
勾股定理;
矩形的性质;