1.
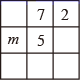
幻方历史悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方.将9个数分别填入如图所示的幻方中,要求每一横行、每一竖列以及两条对角线上的3个数之和都相等,则图中x 的值为.

【考点】
一元一次方程的实际应用-数字、日历、年龄问题;