1.
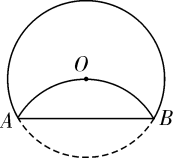
已知⊙O的半径为2,∠AOB=120°.
(1)点O到弦AB的距离为 ;.
(2)若点P为优弧AB上一动点(点P不与A、B重合),设∠ABP=α,将△ABP沿BP折叠,得到A点的对称点为A';
①若∠α=30°,试判断点A'与⊙O的位置关系;
②若BA'与⊙O相切于B点,求BP的长;
③若线段BA'与优弧APB只有一个公共点,直接写出α的取值范围.


【考点】
垂径定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练